Pages du site
Cours actuel
Participants
Généralités
Rappel du fonctionnement d'un ordinateur
...u système d'exploitation Antix (linux) sur clé USB
Les images numériques
Le son
L'architecture client serveur
créer des pages web
Les jeux vidéos
Section 8
Section 9
Section 10
Fiche de notions ICN – Le son
Le numérique nous entoure!
Facile
à stocker, facile à copier, offrant des possibilités d’exploitation et
de traitement importantes, le numérique a su se rendre indispensable, et
ce dans tous les domaines.
Mais comment fait-t-on pour numériser un son ?
On utilise pour ce faire, un convertisseur analogique/numérique (CAN).
Deux paramètres vont régir la numérisation du son, au sein de ce convertisseur :
- La fréquence d’échantillonnage : définition temporelle
- La quantification : définition d’amplitude
|
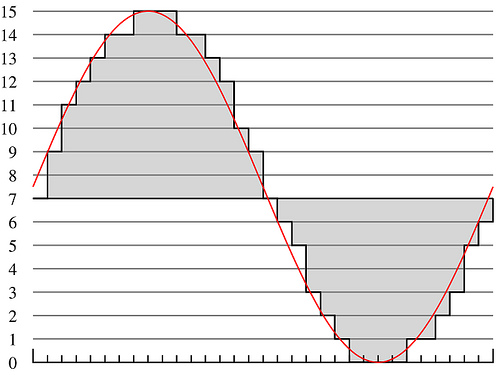
Selon la méthode PCM (Pulse Coded Modulation/Modulation d’impulsion codée), qui est le standard en audionumérique (ainsi qu’en téléphonie), on va relever à intervalles réguliers la valeur de l’amplitude de la forme d’onde et coder cette valeur en langage binaire. En rouge la forme d'onde analogique, en noir sa représentation numérique. On remarque que l'amplitude ne peut prendre qu'un nombre de valeurs fini. (Dans cet exemple, 16) |
Fréquence d'échantillonnage
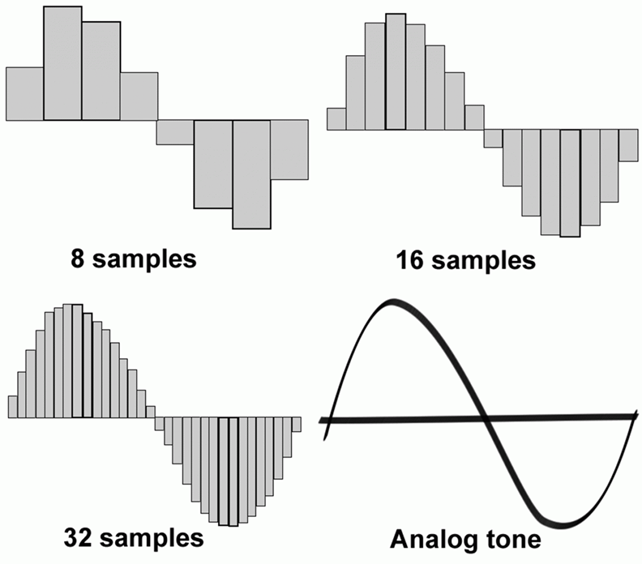
La fréquence d’échantillonnage détermine le nombre d’analyses par seconde. Plus elle est élevée, plus la définition temporelle sera bonne, et plus le résultat sera fidèle à l’onde de départ.
|
Selon le théorème de Nyquist-Shannon, pour qu’il n’y ait pas de perte flagrante, la fréquence d’échantillonnage doit être au moins deux fois plus élevée que la fréquence maximale contenue dans le son à numériser.
|
À l'origine, un signal sonore, c'est de l'air qui vibre. La source sonore est un objet oscillant, qui va transmettre sa vibration aux molécules d'air l'entourant. À leur tour, ces molécules vont entraîner dans leur mouvement leurs voisines, et la vibration va ainsi se propager dans l'espace : c'est ce que l'on appelle une onde sonore. Ce mouvement peut être capté par le tympan de nos oreilles, ce qui nous permet d'entendre les sons. Mais il peut aussi être transmis à la membrane d'un micro : il sera alors transformé en un signal électrique, dont la tension variera au même rythme et avec la même amplitude que la vibration de la membrane. Ce signal électrique est un signal dit analogique ; concrètement, cela signifie que sa valeur est changeante à tout instant.
|
|
|
|
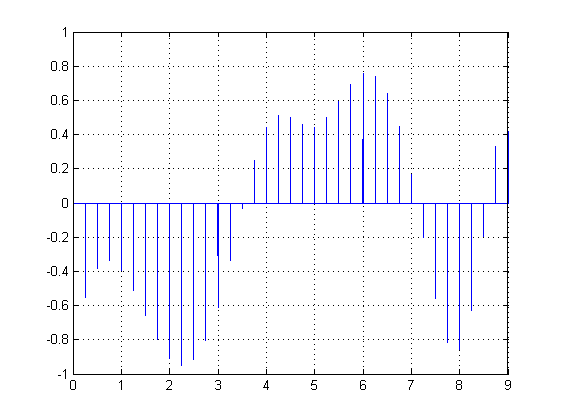
À l'inverse, un signal numérique est, par définition, un signal discontinu, ne changeant de valeur qu'en des instants précis. Pour pouvoir représenter le signal sonore sous forme numérique, on doit le transformer en un signal discret : une suite finie de valeurs bien distinctes les unes des autres. Pour ce faire, on procède à l'échantillonnage de notre signal analogique. On divise chaque seconde en X intervalles de durées égales, et on prélève la valeur du signal au début de chaque intervalle. Le nombre X, noté en Hertz (Hz), s'appelle la fréquence d'échantillonnage. Le résultat de ce processus est un signal ne prenant de valeurs qu'en des instants bien précis. |
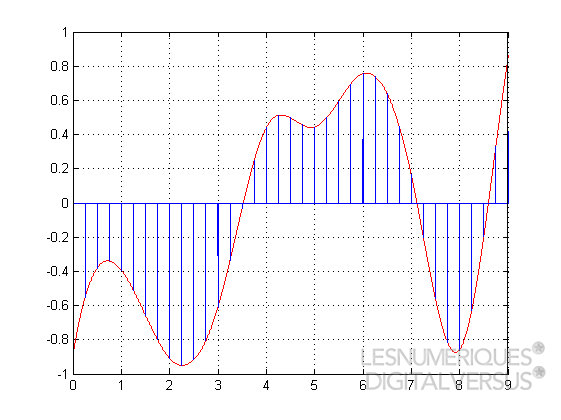
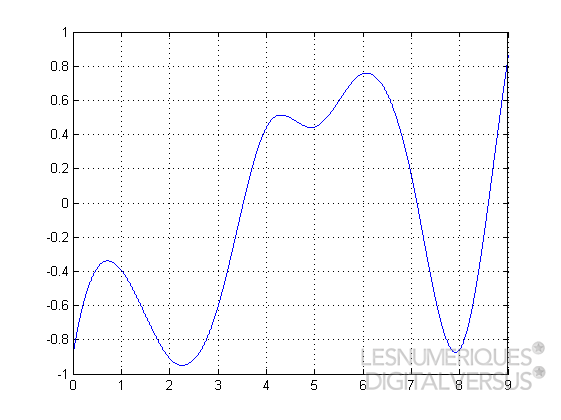
Le problème, on le constate bien, c'est que les détails les plus fins de l'onde sonore ne sont pas conservés : les micro-variations se produisant entre deux instants d'échantillonnage passent nécessairement à la trappe. De fait, ce sont les fréquences les plus élevées du signal sonore qui sont perdues. Pour une fréquence d'échantillonnage F, on ne saura reproduire correctement que les fréquences sonores inférieures à F/2 : c'est ce qu'énonce le théorème de Shannon-Nyquist.
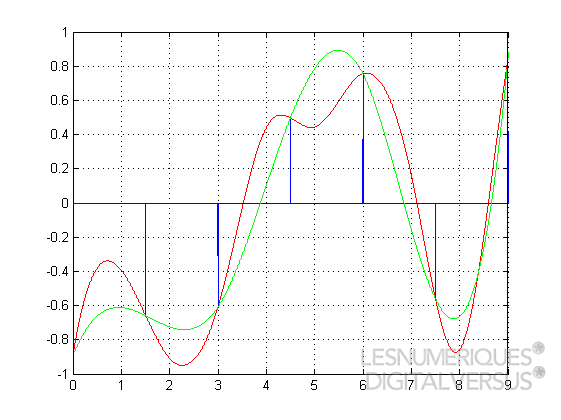
Ici,le signal est violemment sous-échantillonné. On voit, en vert, le signal reconstitué après une conversion analogique → numérique → analogique. À cause de la fréquence d'échantillonnage trop faible, la "bosse" présente dans le signal d'origine au niveau du marqueur 4 a totalement disparu du signal reconstitué. Globalement, on voit bien que le signal reconstitué s'éloigne assez sensiblement du signal d'origine. |
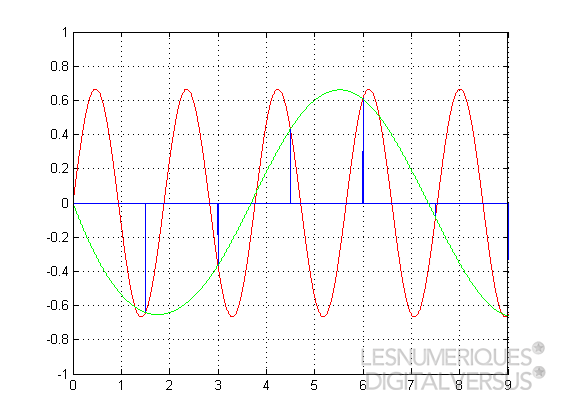
Le signal d'origine, en rouge, a une fréquence supérieure à la fréquence limite de Shannon. Le signal reconstitué, en vert, est « replié » à une fréquence inférieure. Mais alors, qu'advient-il des fréquences supérieures à cette limite, présentes dans le signal d'origine ? Sont-elles totalement perdues ? Eh bien non. Elles sont elles aussi reproduites... mais pas de la bonne façon. En fait, elles sont transformées en des fréquences plus basses, bel et bien inférieures, elles, à la limite de Shannon-Nyquist. Ce phénomène, que l'on appelle le repliement de spectre (ou « aliasing » en anglais), est illustré dans la figure suivante : |
Audio HD : pourquoi augmenter la fréquence d'échantillonnage ?
On considère en général qu'un être humain ayant une excellente oreille perçoit les sons jusqu'à 20 kHz.
Petit calcul rapide : il faudrait donc une fréquence d'échantillonnage supérieure à 40 kHz pour couvrir tout le spectre audible. C'est pour cela que les concepteurs du CD se sont fixés à 44,1 kHz.
Mais dans ce cas, pourquoi vouloir augmenter cette fréquence ? Plusieurs raisons à cela. La première, c'est que les filtres anti-aliasing que l'on utilise dans l'audio sont loin d'être parfaits : ainsi, si l'on veut couper totalement les fréquences supérieures à 22,05 kHz, cela se traduira par une atténuation présente dès 17 kHz environ ; une fréquence qui commence à rentrer dangereusement dans le spectre audible.
Passons l'échantillonnage à 96 kHz : il n'est alors plus nécessaire que de couper les fréquences sonores supérieures à 48 kHz, ce qui nous installe confortablement au-delà de la limite perceptible par l'oreille humaine.
Et le 192 kHz, alors ? Si à 96 kHz, on dépasse déjà largement le seuil de l'audible, pourquoi vouloir monter encore plus haut ? En vérité, cette fréquence n'est jamais réellement utilisée que par les professionnels.
Pour eux, cela fait sens, car les
sons qu'ils manipulent vont subir une multitude de traitements divers
(conversions, filtrages, égalisations...) avant d'être délivrés au
public.
Quantification
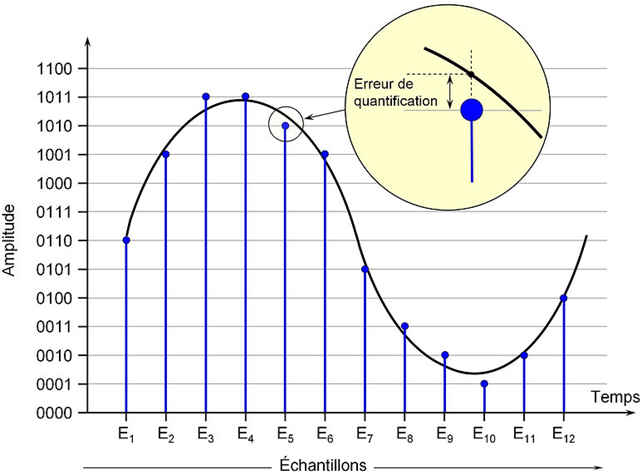
L’amplitude relevée à chaque étape va être codée en binaire sur un certain nombre de bits : 8, 16, 24, 32… C’est la quantification.
Donc, plus on a de niveaux, plus l'erreur de quantification sera réduite. Le choix du pas de quantification correspond à la précision que l'on va accorder au signal. Plus la précision voulue sera grande, plus on aura besoin d'un grand nombre de bits pour coder le signal, plus son poids informatique sera grand. |
|
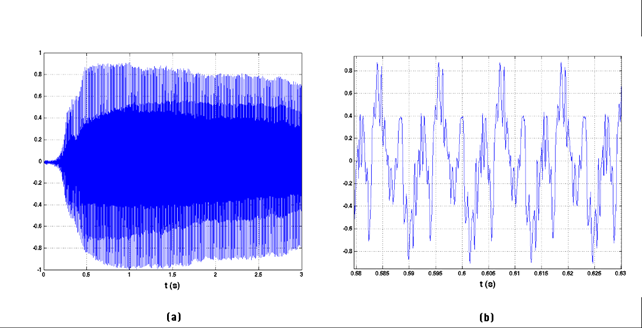
Dans cette partie, on s'intéresse à un signal audio représentant simplement une note tenue dans le temps. C'est un fa joué à la clarinette (87,3 Hz). Ce signal a préalablement été échantillonné à une fréquence de 11 025 Hz. On va maintenant attribuer une valeur numérique à chacun de ces échantillons.
|
Nous allons maintenant jouer sur différents pas de quantification pour numériser ce signal. Le signal original a une amplitude normalisée entre 1 et -1. Nous allons quantifier ce signal à l'aide successivement de 2, 3, 4 ,6 et 8 bits. On rappelle qu'avec 1 bit on a accès à deux niveaux : 0 et 1. |
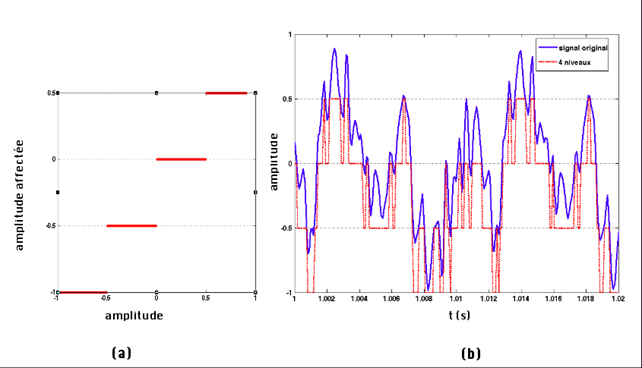
Quantification sur 2 bits(a) niveau affecté au signal numérisé en fonction du signal original, ici 4 niveaux disponibles codés sur 2 bits, (b) signal quantifié sur 2 bits (rouge). |
|
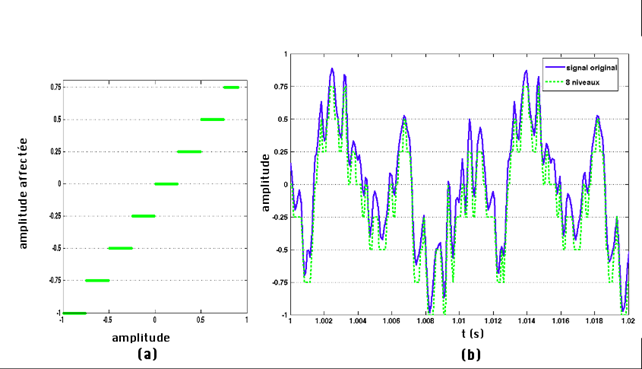
Quantification sur 3 bits(a) niveau affecté au signal numérisé en fonction du signal original, ici 8 niveaux disponibles codés sur 3 bits, (b) signal quantifié sur 3 bits (vert). |
|
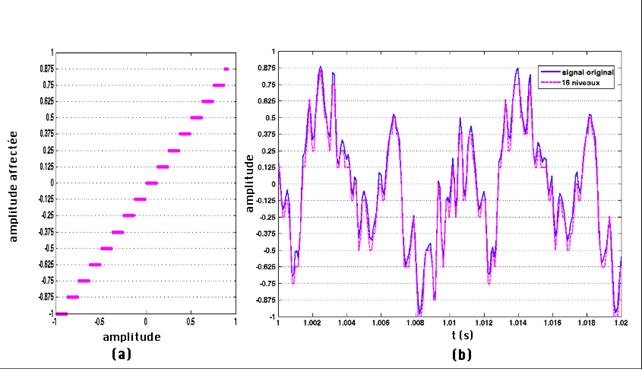
Quantification sur 4 bits(a) niveau affecté au signal numérisé en fonction du signal original, ici 16 niveaux disponibles codés sur 4 bits, (b) signal quantifié sur 4 bits (magenta). |
|
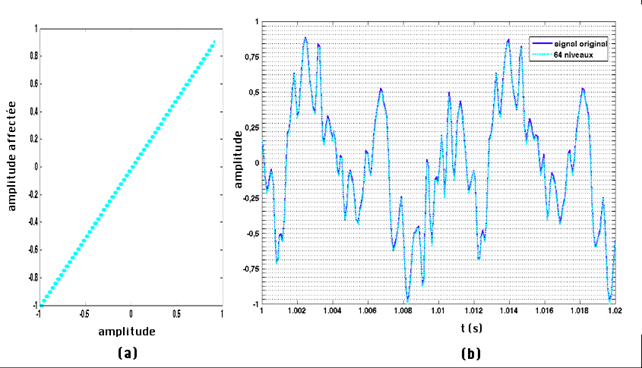
Quantification sur 6 bits(a) niveau affecté au signal numérisé en fonction du signal original, ici 64 niveaux disponibles codés sur 6 bits, (b) signal quantifié sur 6 bits (cyan). |
|
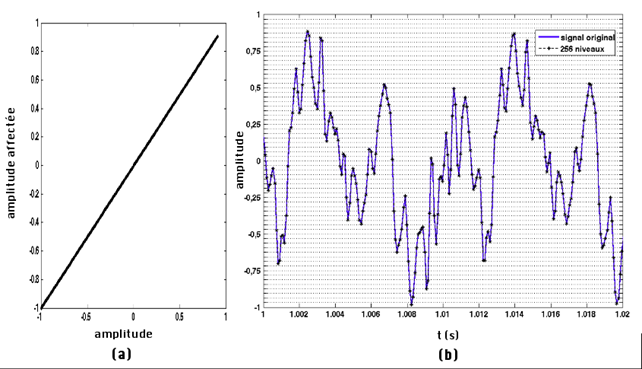
Quantification sur 8 bits(a) niveau affecté au signal numérisé en fonction du signal original, ici 256 niveaux disponibles codés sur 8 bits, (b) signal quantifié sur 8 bits (étoiles noires). |
|
Dans la pratique, pour un enregistrement sur CD Audio, l'audio est codé sur 16 bits, c'est à dire 65 536 niveaux.
Sur le réseau de téléphonie numérique, la voix est codée sur 8 bits. Dans les DVD audio on alloue 24 bits pour coder le son.